Appreciating fuel management, wanting more
Gizmo is fenders down, awning up, in bustling Baltimore Harbor, and I have tales to tell. This old powerboat sails! That’s no surprise given her windage, but now I have precise data about how much wind (and current) can help her along, thanks to a fuel management system. In this photo, for instance, we were making around 10 knots over the ground at 1,350 RPM but still getting over three miles to a gallon, thanks to a stiff easterly wind pushing us down Long Island Sound. That’s a wake-pulling, inefficient RPM when running on flat summer water in Maine, but is much easier on crew and autopilot when in seas like these. While I’m usually willing to spend more fuel money to shoulder through conditions like this, I was pleased to learn that the dollar difference wasn’t great…
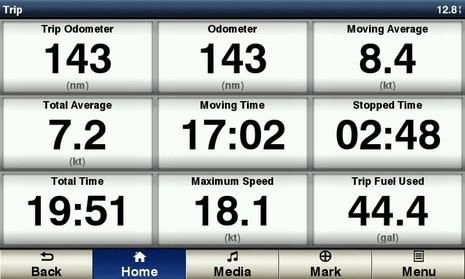
I failed to get a photo of this underway (and may never learn to dust before snapping), but this was our default flybridge engine screen. In the scene I described, the Fuel Economy value — nautical miles per hour divided by realtime gallons of diesel per hour burned by engine(s) — was wavering around 3.1 nm/gal. As explained when I installed the Maretron fuel flow system, measuring instantaneous flow accurately is very hard, especially when a diesel is being run at a relatively small percentage of its maximum power. I’ve learned from the flow meters that my 450 hp Volvo Penta was sucking in about 36 gallons of fuel per hour during that 1350 RPM run, but sending about 33 gallons back to the tank. Set your sink faucet to fill a gallon jug in 20 minutes and you’ll see what a small flow the Maretron gear was trying to measure in realtime, then consider the accuracy difficulty when that flow is actually the differential of two flows ten times greater.
So I’ve gotten used to seeing jiggelty fuel economy numbers, but find them valuable nonetheless. The fuel burn at different RPMs in still conditions is generally consistent, and all summer I noticed how I could see the effect of fair or foul winds and currents. Besides, the difficulty of measuring instantaneous flow doesn’t mean these meters aren’t extremely accurate over longer periods…
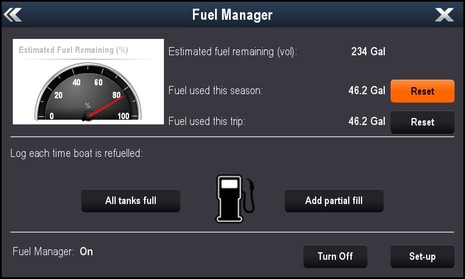
I have reasons to believe that Gizmo did indeed use 238 gallons of fuel steaming from Rockland to Baltimore. For one thing, this Garmin GMI20 totals fuel flow independently, but is within a (rounding error) gallon of the count kept by the Maretron system itself. Moreover, the Garmin calculates Fuel Onboard by subtracting flow from the total you told it was onboard when the trip started plus what you record as added later. So a full 280 gallon load (at a nice price, thanks to Journey’s End Marina’s fuel key program) plus 115 gallons added at fabulously funky Miss Chris Marina in Cape May equals 395 gallons, less 238 used equals (rounding error) 157 remaining.
Ah, but you skeptics out there are wisely thinking, “Wait, the counting may be independent but isn’t it all based on a single source of fuel flow data?” Which is why I was pleased to learn that Maretron does not calculate remaining fuel using flow, but instead does it based on tank capacity and level. Right now it reads 159 gallons remaining, which is darn close for an entirely different way to measure fuel volume. Skeptics must conclude that either the Maretron flow system and the tank calibration I did using a CZone Signal Interface (using existing Wema senders) are both quite accurate…or they err in a currently copacetic way.
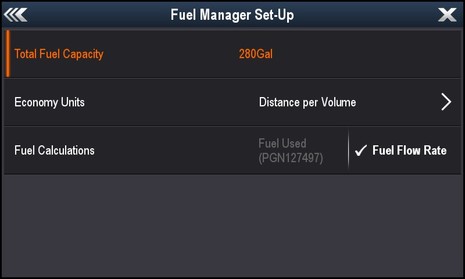
There are many aspects to fuel management and potentially many sensors and confusions involved. This screen shows how Raymarine let’s you choose to display gallons used and remaining by either counting the flow rate like Garmin does — the Ray a77 warns that it must always be on when the engine is running — or by referencing NMEA 2000 PGN 127497. That set of data fields is called “Trip Parameters, Engine” and the Maretron FFM100 module is always transmitting a current “Trip Fuel Used” count.
I don’t know why, but you can only start the Ray fuel manager when you’ve done a fill up (and already set up the tank capacity). I did all that in Rockland, but somehow the manager got reset somewhere along the road; it may have been operator error, but I won’t be able to get it right again until I do a full fill. However, my extensive paper records indicate that Raymarine can count fuel flow well and, like other displays, their MFDs can also calculate range and/or running hours at a given RPM. My records are revealing some oddities, too, like the way the Actisense EMU-1 (discussed here) adds engine hours when it’s on but the engine isn’t running.
There will definitely be another entry on fuel management as I learn more about it and try other data displays. But I should mention the unfortunate fact that at least one of my Maretron flow sensors is weeping about a gallon of fuel per month into Gizmo’s engine pan. I don’t know if it’s because I didn’t screw an NPT fitting tight enough into a meter’s resin body, or so tight that it caused a crack. Maretron says that either is possible and admits that the tolerance either way is slim, but also says they’ve never seen a catastrophic failure (sensor blows apart, bad things ensue). Plus, most of their current sensors — click on “Accessories” tab, and note that they’ve added models for really large flows — now have aluminum bodies.
I look forward to switching flow sensors so I don’t have to mess with spilt fuel, and I also look forward to displays that make even better use of flow information. For instance, none that I know of can collect an average nm/gal figure for a trip. And I haven’t yet seen the “money meter” I’ve joked about (and that Maretron is purportedly working on). A display system just needs to be able to accept the per gallon price when you input a fill and it could then give you realtime and trip time cost per mile…if you want to know.
I can crunch a spreadsheet, though, and have enough data to tell you that Gizmo averaged 3.1 nm/gal over the 740 mile trip at a fuel cost of $0.87 per mile. Most of those miles were at more than penny-pinching RPMs, but very few at mile-per-gallon 17 knots. Plus, we got more than our share of tail winds and also tried hard to time the currents, even leaving Atlantic Highlands at 4 am. Sailors can justifiably scoff at my fuel “efficiency,” but then again we enjoyed briefly catching up with a couple of big 20k+ power yachts, because they apparently had to refuel in Atlantic City (or gamble a bit). Yet then again, those guys might enjoy seeing a big number on their “money meter”; we’re not all the same and I’m OK with that.















A few years ago I purchased the first generation of FloScan’s NMEA 2000 system called FloNet. The fuel sensors plumbed into the supply and return are gigantic and look like the size of oil filters, but seem to be very accurate when used with my 50 Hp Yanmar engine aboard our Tashiba 40 sailboat.
This summer I made the same trip down the NJ coast from Long Island. When I refueled in Atlantic City at Kammermans Marine I had calculated needing 35.5 gallons of diesel based on the FloNet “Total Fuel Remaining” . When we shut off the fuel dispenser, the pump read 35 gallons. I was surprised and mentioned out loud that I was expecting it to take 35.5. A guy on the dock sarcastically replied, “you better check your math” . We got a good laugh out of the comment. The accuracy of one gallon to as good as a half gallon at each fill was repeatable all summer.
I think the next improvement is to reduce the size of the fuel sensors and insure that the low fuel flow on small diesel engines remain accurate.
Ben – slightly off topic… Can you share what sort of sensor you’re using to measure engine RPM and get it on the NMEA network? Thanks.
Ben,
Regarding the fuel leak, try Leak Lock:http://www.highsidechem.com/leaklock.html
I’ve been using the earlier composite flow sensors
& tightening the fittings is tricky. Try Leak Lock
by HighSide Chemicals for a leak free connection,
or, alternatively, teflon tape. But not the usual thin as toilet tissue type. MIL spec or HD pink will do & if properly applied leaving 2~3 leading threads bare & properly wound will do it with no migration into the fuel system & no leaks–+ no cure time & surfaces, while clean is best, do no have to be as pristine as using a liquid sealant.
Holy smoke, Ben – I think we have the same dinghy.. mine is much more beat up, though (raised two girls around her). Do you sail her, too?
Hey, Hartley, that’s a Fatty Knees 9 (they also make 7 and 8 foot models) I was very pleased to acquire in August. It definitely sails, even with two old “robust” guys onboard, and also rows and Torqeedo’s well. It also fits well on Gizmo and I can haul/launch quickly and easily. I plan to write an entry about it eventually.
John, thanks very much for the leak advice; Leak Lock on order!
Evan, an Actisens EMU-1 is converting analog RPM and more to N2K. Install entry here: http://goo.gl/rKNegz
Richard, great to hear that you’re experiencing such fuel management perfection, but I’m going to keep paper cross tabulations for a while. Just stumbled on a reference to my friend Peter Swanson almost running out of fuel apparently due to electronic FM gone wrong:
http://www.powerandmotoryacht.com/cruising/down-east-loop-day-11
The whole series of entries about different magazine writers taking a Cutwater 28 around the Down East Loop is fun (and now the boat is headed here to TrawlerFest):
http://www.powerandmotoryacht.com/voyaging/cruising
Hi Ben – Exactly! We, too, have a Fatty Knees 9 – bought it in 1995 from Edey & Duff. Ours has a lot more scratches and gouges than yours does, but she’s still going strong. Both of our daughters had a lot of wonderful hours of rowing and sailing in her, and she’s never tipped us out..:-) Good to hear that they work well with the Torqueedo – that’ll be our next motor, as the olde Johnson packed it in last year..:-(
Mine’s also an Edey & Duff, circa 1993, and has many dings that don’t show in the photo. Amazingly stable. I stopped in Pocasset, Cape Cod, on the way down to pick up a set of teak floorboards from the current manufacturer. Nice guy.
http://www.fattyknees.com
Given its importance, it seems surprising that the major manufacturers have devoted relatively little thought to integrating fuel management. Newer electronically controlled common rail Diesels such as the Cummins QSBs in my boat can put accurate realtime fuel rate data onto a NMEA 2000 network with no need for the complexity and plumbing you had to do with a mechanical injection system. Of course I had to figure out how to do it myself. Cummins still uses on the Mercury VesselView displays but since their break with Mercury gets no support. They tried to help me but no one knew how to get the data out of the engines. However, I bit the bullet and experimented with a Mercury interface box and it miraculously worked.
Then I discovered that my Simrad NSE plotters could not do anything other than show the live fuel rate and fuel economy — no ability to store data and calculate fuel consumed and fuel remaining. After a long discussion with thier tech support, I was advised to put a Lowrance EP85 on the network to store the data. Wrong — that was a complete failure. It would multiply the fuel rate by about 100 so my tank was down to empty in minutes.
Finally I got a Garmin GMI-20, which does a very good job of tracking consumption for me as it does for you. I get repeatable accuracy from fill to fill of around 1-2% on 280 gallons, which may be partially due to temperature differences affecting the volume of fuel the tank can hold. Garmin needs to allow for two or better three decimal places on the fuel economy for those of us with inefficient boats. My cruising rate is around 0.80nmpg but can go down to 0.74 or up to 0.84 with small changes in trim tabs or speed. That all shows up as 0.8 on the GMI-20, which only shows tenths.
By the way, the Cummins VesselView does have some of the capabilities you discussed. It will tabulate average fuel economy for a resettable trip and even calculate and display fuel to an active waypoint. It should be very easy for Simrad to do the same on the NSE but they did not bother to write the software.
I am amazed at the accuracy of your fuel tank readings. My analog gauge is pretty accurate — sitting at the dock. Once underway, it is completely useless as the running angle an attitude of the boat shifts. Am I missing a trick?
Thanks, Quitsa, interesting comment. Did you know that Navico builds the VesselView displays for Mercury and last year both showed off some tight integration between the newer VV and evo2 displays?
https://panbo.com/archives/2014/02/miami_2014_glass_bridge_everywhere.html
I haven’t tried fuel management on the NSS evo2’s yet — they’re on a different N2K network — but it seems similar to what Raymarine and Garmin are doing.
Incidentally, the Maretron fuel remaining based on tank level figure I used was observed at rest. It also may be a lucky number. Going down the road I’ll check how it compares underway, though Gizmo has long, tall, narrow fuel tanks so the senders don’t seem to fluctuate wildly in a seaway.
On the other hand, I managed to jam the port tank sender nearly to the tank bottom when fueling with a high capacity pump in Rockland. Of course I was showing off how I could see tank levels on my iPad as I fueled (via Garmin Helm) to my mate Joe when the tank level went from around 85% to 23%…and stayed there! Back to the old “listen to the vent” method. As hoped the sender squared itself away that night when we did a little pounding.
Incidentally, none of the fuel management I’ve tried so far deals with individual tanks. They typically ask how many tanks you have and the total capacity but fuel remaining, range, and time remaining are based on total fuel on board. I’m fine with that as I think it would get too complicated to do otherwise, plus I sometimes use my fuel return valve (carefully) to move diesel from one wing tank to the other to maintain even trim.
Quitsa – I agree completely with your statements on the GMI20’s lack of decimal precision when it comes to fuel flow – but I’m not optimistic about getting any improvements from Garmin. Following is from an Oct 2012 email to a regional tech representative from Garmin concerning the GMI20’s predecessor, the GMI10:
“Fuel Flow only calculates/displays NMPG to one decimal place: I’m not a big fan of unnecessary precision, but this is one place where we REALLY need to have an extra decimal place displayed. Virtually all cruising vessels have fuel economies of less than 2 NMPG (Nautical Miles Per Gallon), and many achieve less than 1 NMPG. When the GMI10 displays a fuel economy of 0.8 NMPG, I can only assume the actual economy is somewhere between .75 and .84 (in other words, rounded to the nearest 1/10 of one mile per gallon). But with these small numbers, that represents a BIG difference – in fact, it’s over 10 percent! With today’s fuel costs, I would be thrilled to improve my economy by 10 per cent! We really need more precision here. Adjusting engine speed in 100 RPM increments can yield a very precise “best economy cruise” setting, but ONLY if the instrumentation allows us to see it.”
I thought I stated my case pretty well back then – apparently the folks at Garmin remain unimpressed. I think it’s great Ben gets 3+ NMPG in Gizmo, but that’s really the exception among power cruisers over 30 feet or so.
The whole issue of decimal place precision really irks me, with some manufacturers providing WAY too MUCH precision (heading to the 10th of a degree, Lat/Lon to 4 decimal places), creating busy displays with numbers constantly jumping around to no use – and in this case, clearly not enough. I just don’t get how they can miss obvious stuff like this with even a cursory amount of real-world testing.
Was at the pump yesterday.
Max fuel is 400 litres.
Guy asked how much I told him 192 litres
GMI20 was at 208 remaining.
At auto shut off the fuel pump at the diesel station said 193 litres.
Close enough for me.
Fuel flow is alway’s that accurate.
Floscan Flonet and GMI20 and Simrad.
Simrad (EP85R) is having Alzheimer or so.
It keeps forgetting the fuel remaining after a few hours or day’s (at the longest).
Navico is working on the solution
In use The Simrad’s are working great and represent a 2 decimal fuel flow figure (km/Litre).
Yhis wil give me the possibility tot optimal Engine/Trimtabs trim in combination with the best RPM setting
My Simrad NSE will display fuel economy (with two decimal places). What it won’t do is store a total of fuel consumed as the Garmin GMI-20 does. It would be nice to use a single piece of hardware for both functions.
I concur in Grant’s comment about precision. It should be not that hard to allow a user setting just as you can choose between metric and English units. I had a similar interaction with Furuno a number of years ago because the NavNet on my old boat would only display tenths for sea temperature. They did modify the software in the next update to allow for two decimal places.
You can connect a EP 85r fuel memory module in your n2k network. That should remember the fuel remaining.
Not yet on my system, but the a working on it to fix it.
The EP85R most assuredly does not correctly store fuel data when used with an NSE display. It may work with Lowrance hardware or in other configurations. I speak from direct experience, which was confirmed by Simrad tech support after some struggle on my part. Perhaps this was fixed in the most recent software. I was trying it about a year ago.
Forgot to add that it does store fuel use data, it’s just wildly inaccurate.
No it is not fixed yet, but when working it is as accurate as the GMI20